1. 矩阵求导的本质:
矩阵A对矩阵B求导,矩阵A中的每一个元素分别对矩阵B中的每一个元素进行求导。
$\frac{d f(x)}{d x}$
$A_{1 X 1}$ $B_{1 X 1}$ 1个导数
$A_{m X 1}$ $B_{1X1}$ m个导数
$A_{mX1}$ $B_{pX1}$ mxp 个导数
$A_{mXn}$ $B_{pXq}$ mxnxpxq 个导数
1. 标量函数
$[f]_{1 X 1}$
$f(x)=x$
$f(x_1, x_2) = 2x_1 +3x_2^2$
2. 向量函数
$[f]_{m X n}$
$[f_1(x) = x, f_2(x) = x_2]_{1 X 2}$
2. 以分母布局为例的矩阵求导的基本原则
所谓以分母布局,就是说求导后的形状和分母的形状保持一致。
$\frac {\partial{f} \leftarrow 分子}{\partial{x} \leftarrow 分母}$
原则:
-
分子为标量,分母为向量,求导结果同分母的形状。
$f$ :标量函数
$x$ :列向量
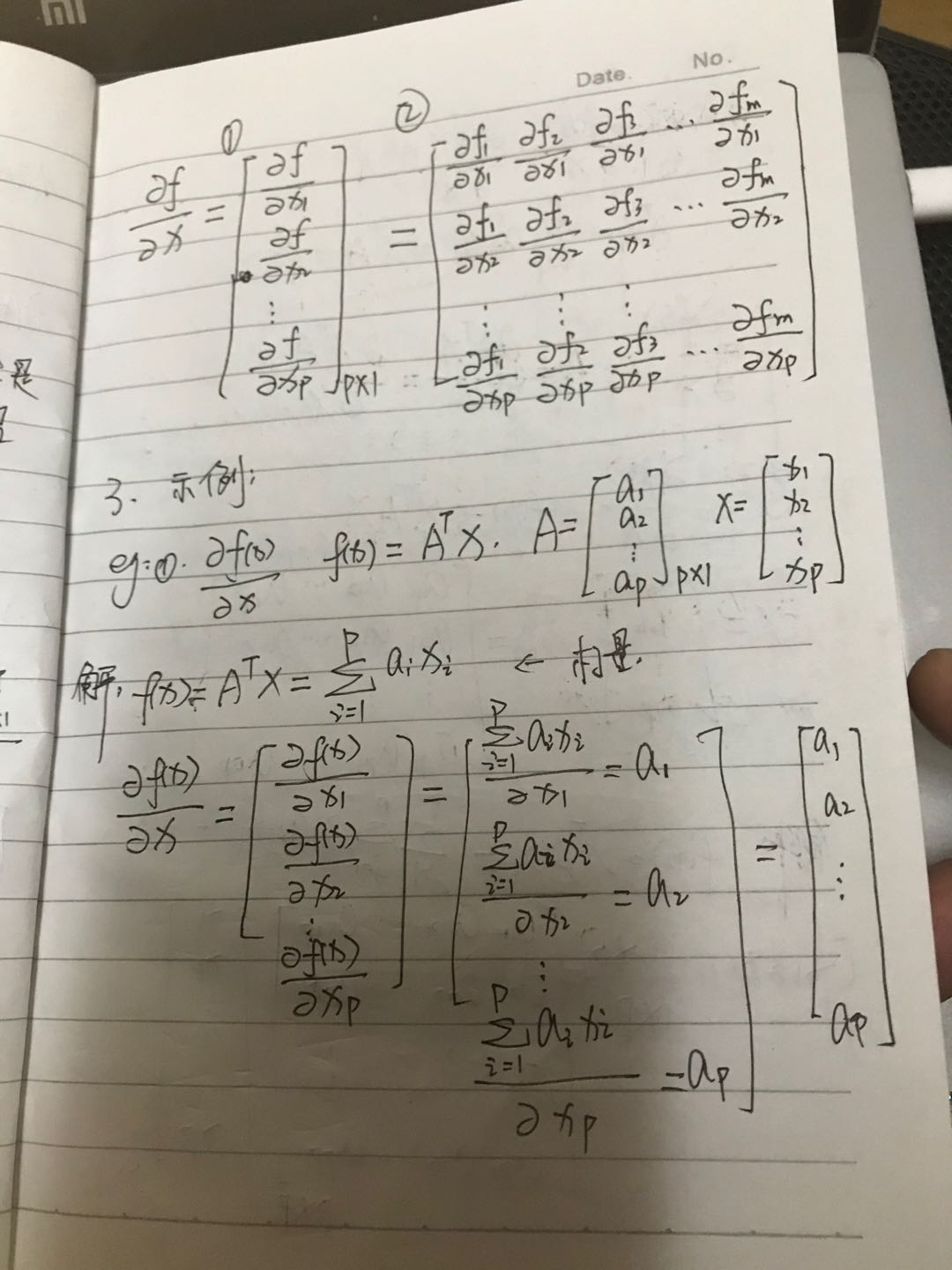
书写latex公式太慢了,先将笔记图片拍照放这里,后续有空了,再整理。